RBFE¶
This document describes how to run a RBFE simulation using Deep Origin tools.
Prerequisites¶
We assume that we have an initialized and configured Complex object:
from deeporigin import drug_discovery as dd
sim = dd.Complex.from_dir("/path/to/folder/")
sim.connect()
Starting an RBFE run¶
Single pair of ligands¶
To run an end-to-end RBFE workflow on a single pair of ligands, we use:
sim.rbfe.run_end_to_end(
ligand1_id="Ligands-1", # for example
ligand2_id="Ligands-2",
)
This queues up a task on Deep Origin. When it completes, outputs will be written to the appropriate column in this database.
You will see a message printed to screen similar to:
Expected output
🧬 Job started with ID: 20f05e96, execution ID: x9rl5eghrpqwyiciehc3e
Constructing a network¶
Coming soon
Ability to construct a network of ligands for RBFE is coming soon.
Parameters¶
The end to end RBFE tool has a number of user-accessible parameters. To view all parameters, use:
sim.rbfe._params.end_to_end
Expected output
This will print a dictionary of the parameters used for RBFE, similar to:
{
"complex_prep": {
"include_ligands": 1,
"include_protein": 1,
"sysprep_params": {
"charge_method": "bcc",
"do_loop_modelling": false,
"force_field": "ff14SB",
"is_lig_protonated": false,
"is_protein_protonated": false,
"keep_waters": false,
"lig_force_field": "gaff2",
"padding": 1.0,
"save_gmx_files": false
},
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0
},
"ligand1_prep": {
"include_ligands": 1,
"include_protein": 0,
"sysprep_params": {
"charge_method": "bcc",
"do_loop_modelling": false,
"force_field": "ff14SB",
"is_lig_protonated": false,
"is_protein_protonated": false,
"keep_waters": false,
"lig_force_field": "gaff2",
"padding": 1.0,
"save_gmx_files": false
},
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0
},
"ligand2_prep": {
"include_ligands": 1,
"include_protein": 0,
"sysprep_params": {
"charge_method": "bcc",
"do_loop_modelling": false,
"force_field": "ff14SB",
"is_lig_protonated": false,
"is_protein_protonated": false,
"keep_waters": false,
"lig_force_field": "gaff2",
"padding": 1.0,
"save_gmx_files": false
},
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0
},
"rbfe": {
"add_fep_repeats": 0,
"amend": "__NO_AMEND",
"annihilate": true,
"atom_mapping_threshold": 0.01,
"em_all": true,
"em_solvent": true,
"emeq_md_options": {
"T": 298.15,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"Δt": 0.004
},
"fep_windows": [
{
"restraints_A": [
0.0,
0.01,
0.025,
0.05,
0.1,
0.35,
0.5,
0.75,
1.0
]
},
{
"coul_A": [
1.0,
0.8,
0.6,
0.4,
0.2,
0.0
]
},
{
"vdw_A": [
1.0,
0.9,
0.8,
0.7,
0.6,
0.5,
0.4,
0.3,
0.2,
0.1,
0.0
]
}
],
"mbar": 1,
"npt_reduce_restraints_ns": 2.0,
"nvt_heating_ns": 1.0,
"prod_md_options": {
"T": 298.15,
"barostat": "MonteCarloBarostat",
"barostat_exchange_interval": 500,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"integrator": "BAOABIntegrator",
"Δt": 0.004
},
"repeats": 1,
"run_name": "binding",
"skip_emeq": "__NO",
"softcore_alpha": 0.5,
"steps": 1250000,
"system": "complex",
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0,
"threads": 0,
"workers": 0
},
"solvation1": {
"add_fep_repeats": 0,
"amend": "__NO_AMEND",
"annihilate": true,
"atom_mapping_threshold": 0.01,
"em_all": true,
"em_solvent": true,
"emeq_md_options": {
"T": 298.15,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"Δt": 0.004
},
"fep_windows": [
{
"coul_A": [
1.0,
0.8,
0.6,
0.4,
0.2,
0.0
]
},
{
"vdw_A": [
1.0,
0.9,
0.8,
0.7,
0.6,
0.5,
0.4,
0.3,
0.2,
0.1,
0.0
]
}
],
"mbar": 1,
"npt_reduce_restraints_ns": 0.2,
"nvt_heating_ns": 0.1,
"prod_md_options": {
"T": 298.15,
"barostat": "MonteCarloBarostat",
"barostat_exchange_interval": 500,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"integrator": "BAOABIntegrator",
"Δt": 0.004
},
"repeats": 1,
"skip_emeq": "__NO",
"softcore_alpha": 0.5,
"steps": 300000,
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0,
"threads": 0,
"workers": 0
},
"solvation2": {
"add_fep_repeats": 0,
"amend": "__NO_AMEND",
"annihilate": true,
"atom_mapping_threshold": 0.01,
"em_all": true,
"em_solvent": true,
"emeq_md_options": {
"T": 298.15,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"Δt": 0.004
},
"fep_windows": [
{
"coul_A": [
1.0,
0.8,
0.6,
0.4,
0.2,
0.0
]
},
{
"vdw_A": [
1.0,
0.9,
0.8,
0.7,
0.6,
0.5,
0.4,
0.3,
0.2,
0.1,
0.0
]
}
],
"mbar": 1,
"npt_reduce_restraints_ns": 0.2,
"nvt_heating_ns": 0.1,
"prod_md_options": {
"T": 298.15,
"barostat": "MonteCarloBarostat",
"barostat_exchange_interval": 500,
"cutoff": 0.9,
"fourier_spacing": 0.12,
"hydrogen_mass": 2.0,
"integrator": "BAOABIntegrator",
"Δt": 0.004
},
"repeats": 1,
"skip_emeq": "__NO",
"softcore_alpha": 0.5,
"steps": 300000,
"test_run": 0,
"thread_pinning": 1,
"thread_pinning_offset": 0,
"threads": 0,
"workers": 0
}
}
Any of these parameters are modifiable using dot notation. For example, to change the number of steps in the RBFE step, we can use:
sim.rbfe._params.end_to_end.rbfe.steps = 500000
Results¶
Viewing results¶
After initiating a run, we can view results using:
sim.rbfe.show_results()
This shows a table similar to:
Expected output
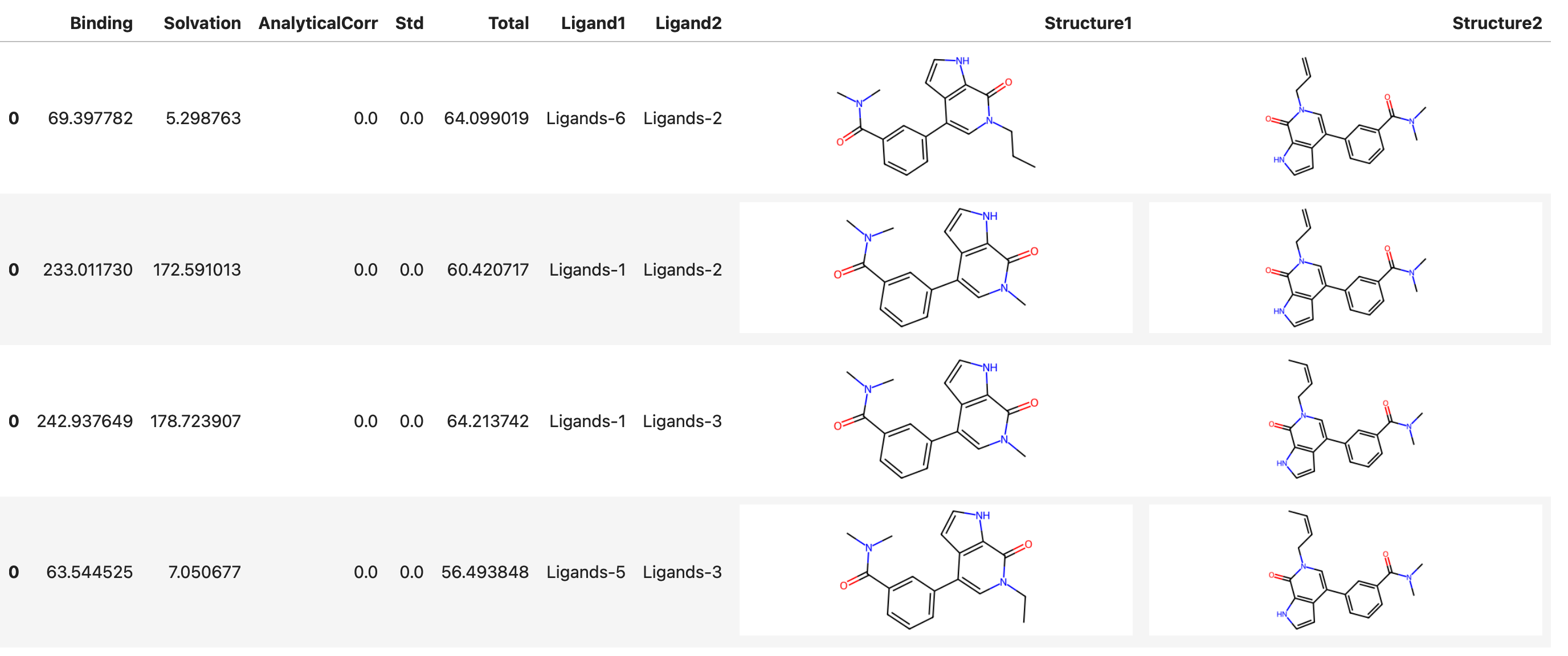
Exporting results for analysis¶
These results can be exported for analysis using:
df = sim.rbfe.get_results()
df
Expected output
| Index | Binding | Solvation | AnalyticalCorr | Std | Total | Ligand1 | Ligand2 | SMILES1 | SMILES2 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 69.397782 | 5.298763 | 0.0 | 0.0 | 64.099019 | Ligands-6 | Ligands-2 | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... | [H]C([H])=C([H])C([H])([H])N1C(=O)C2=C(C([H])=... |
| 0 | 233.01173 | 172.591013 | 0.0 | 0.0 | 60.420717 | Ligands-1 | Ligands-2 | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... | [H]C([H])=C([H])C([H])([H])N1C(=O)C2=C(C([H])=... |
| 0 | 242.937649 | 178.723907 | 0.0 | 0.0 | 64.213742 | Ligands-1 | Ligands-3 | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... |
| 0 | 63.544525 | 7.050677 | 0.0 | 0.0 | 56.493848 | Ligands-5 | Ligands-3 | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... | [H]C1=C([H])C(C(=O)N(C([H])([H])[H])C([H])([H]... |