ABFE¶

This document describes how to run an ABFE simulation using Deep Origin tools.

The ABFE class drives platform tool deeporigin.abfe-end-to-end with ordered workflow steps:

• ["system-prep", "abfe"] — protein + ligand through system prep, then FEP (default)
• ["abfe"] — FEP only on an existing PreparedSystem

Prerequisites¶

We assume that you have prepared a protein, docked a ligand to it, and obtained a pose that you want to proceed with.

In this tutorial we will use a protein and ligand from the example dataset.

from deeporigin.drug_discovery import (
    ABFE,
    ABFEParams,
    BRD_DATA_DIR,
    Protein,
    Ligand,
)

protein = Protein.from_file(BRD_DATA_DIR / "brd.pdb")
protein.sync()

ligand = Ligand.from_sdf(BRD_DATA_DIR / "brd-2.sdf")
ligand.sync()

For more details on how to get started, see Getting Started .

Combined workflow (recommended)¶

Pass protein and ligand to run system preparation and ABFE in one execution:

abfe = ABFE(protein=protein, ligand=ligand)
abfe.start(quote=True)
abfe.estimate

After quoting, confirm and watch progress as shown below. When the system-prep step completes, you can load the prepared system from the same execution:

prepared = abfe.get_prepared_system()
prepared.show()

Two-step alternative (SystemPrep)¶

You can still prepare the system separately with SystemPrep, then submit FEP-only steps=["abfe"]:

from deeporigin.drug_discovery import SystemPrep, PreparedSystem

sysprep = SystemPrep(protein=protein, ligand=ligand)
system = sysprep.run()
system.show()

abfe = ABFE(prepared_system=system)
abfe.start(quote=True)
abfe.estimate

System prep builds two solvated models:

1. Binding system — protein and ligand in explicit solvent (binding leg).
2. Ligand solvation system — ligand alone in solvent (solvation leg).

You will see something like:

Estimating costs¶

Before starting an ABFE run, you can estimate costs using start(quote=True) on either workflow entry point (combined or two-step):

abfe = ABFE(protein=protein, ligand=ligand)
abfe.start(quote=True)
abfe.estimate

You will get back an estimate (in USD) of how much this run will cost.

Starting an ABFE run¶

Confirming a quoted Job¶

To confirm the quoted price and start the execution, do:

abfe.confirm()

This will start the ABFE run. Use the following to monitor the status of the job:

task = await abfe.watch()

You will see a widget similar to this (progress simulated for demonstration):

Parameters¶

ABFE simulation parameters are controlled via the ABFEParams dataclass. Default values are tuned for production runs; most users will only need to adjust a small number of fields.

Viewing parameters¶

To inspect the current parameters on an ABFE object, access the params property:

abfe.params

ABFEParams(
  annihilate: True
  dt: 0.004
  temperature: 298.15
  cutoff: 0.9
  repeats: 3 *
  replex_period_ps: 2.5
  test_run: 0
  binding_n_windows: 48
  binding_npt_reduce_restraints_ns: 2.0
  binding_nvt_heating_ns: 1.0
  binding_steps: 1250000
  solvation_n_windows: 32
  solvation_npt_reduce_restraints_ns: 0.2
  solvation_nvt_heating_ns: 0.1
  solvation_steps: 500000
)

Modifying parameters¶

ABFEParams is a frozen dataclass. Use dataclasses.replace() to build a modified copy and pass it to the constructor:

from deeporigin.drug_discovery import ABFEParams
from dataclasses import replace

params = replace(ABFEParams(), repeats=3, temperature=300)
params

Parameters modified from the defaults are indicated with an asterisk:

ABFEParams(
  annihilate: True
  dt: 0.004
  temperature: 300 *
  cutoff: 0.9
  repeats: 3 *
  replex_period_ps: 2.5
  binding_n_windows: 48
  binding_npt_reduce_restraints_ns: 2.0
  binding_nvt_heating_ns: 1.0
  binding_steps: 1250000
  solvation_n_windows: 32
  solvation_npt_reduce_restraints_ns: 0.2
  solvation_nvt_heating_ns: 0.1
  solvation_steps: 500000
)

Results¶

Viewing results¶

After a run completes successfully, fetch results with:

df = abfe.get_results()
df

This shows a table similar to:

Viewing trajectories¶

To view MD trajectories from this run, refer to ABFE.

Viewing overlap matrix¶

An FEP overlap matrix is a diagnostic used in free energy perturbation calculations to evaluate how well neighboring λ states sample overlapping regions of configuration space. Each matrix element measures the statistical overlap between configurations from different states based on their energy distributions. The goal is to ensure every state has overlap with its neighbors in both directions – so that off-diagonal elements are sufficiently larger than zero.

The plot path is read from the data-platform result for this execution (default repeat=1, same indexing as abfe.show_trajectory). In Jupyter:

abfe.show_overlap_matrix(run="binding")

An image such as the following will be shown:

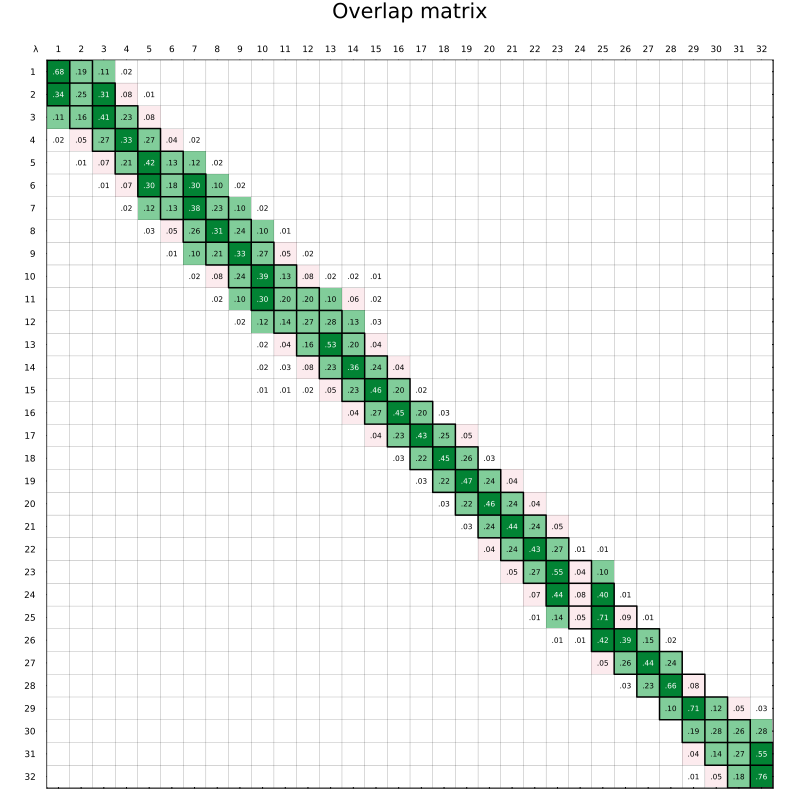
To view the overlap matrix for the solvation leg:

abfe.show_overlap_matrix(run="solvation")

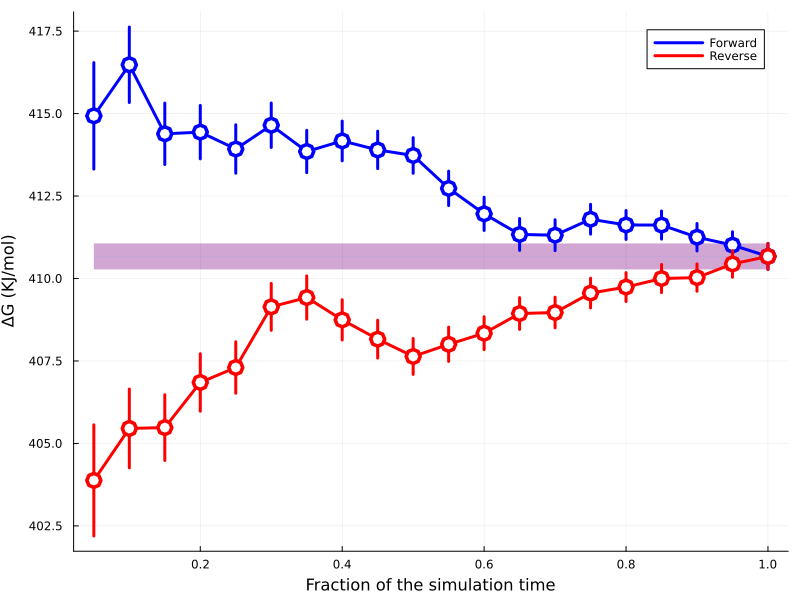
Viewing convergence time plots¶

The time-convergence diagnostic (convergence_plot in the result payload) can be shown the same way as the overlap matrix (default repeat=1, same as abfe.show_overlap_matrix and abfe.show_trajectory):

abfe.show_convergence_time(run="binding")

An image such as the following will be shown:

For the solvation leg:

abfe.show_convergence_time(run="solvation")